问题
单项选择题
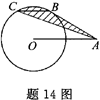
如题14图所示，A是半径为1的圆O外的一点，OA=2，AB是圆O的切线，B是切点，弦BC∥OA，连接AC．则阴影部分的面积等于 ( )．
答案
参考答案：B
解析：
如题14图所示，在△OBC与△ABC中，因BC∥OA，故O到BC的距离与A到BC的距离相等．而这两个三角形共底BC，故
S△OBC=S△ABC．
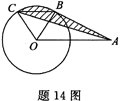
因此所求阴影部分的面积即为圆O中扇形OBC的面积．
在直角△OBA中(因B为切点，故OB⊥AB)OB=1，OA=2，故 COS∠BOA=
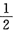，即∠BOA=
，而CB∥OA，故∠CBO=∠BOA=
．所以△OBC为等边三角形，故∠COB=．所以扇形OBC的面积=圆O面积=
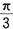π12==所求阴影部分面积．
故正确的选择应为B．