问题
解答题
求下列各函数的最值。
(1)f(x)=-x4+2x2+3,x∈[-3,2];
(2)f(x)=x3-3x2+6x-2,x∈[ -1,1]。
答案
解:(1)f′(x)=-4x3+4x,
令f′(x)=-4x(x+1)(x-1)=0,
得x1=-1,x2=0,x3=1,
当x变化时f'(x)及f(x)的变化情况如下表:
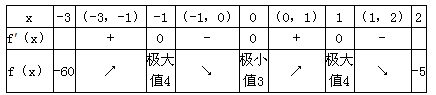
∴当x=-3时,f(x)取最小值-60;
当x=-1或x=1时,f(x)取最大值4;
(2)f′(x)=3x2-6x+6=3(x2-2x+2)=3(x-1)2+3,
∵f′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上为增函数,
故x=-1时,f(x)最小值=-12;x=1时,f(x)最大值=2,
即f(x)的最小值为-12,最大值为2。
