解：(1)f(x)=x²+2x-41nx(x＞0)，f′(x)=2x+2-，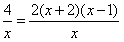

当x＞1时，f′(x)＞0，当0＜x＜1时，f′(x)＜0，

∴f(x)在(0，1)上单调递减，在(1，+∞)上单调递增，

∴f(x)_min=f(1)=3．

(2)，

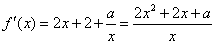若f(x)在(0，1)上单调递增，则2x²+2x+a≥0在x∈(0，1)上恒成立

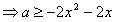在x∈(0，1)上恒成立，

令u=-2x²-2x，x∈(0，1)，则，，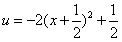

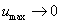∴a≥0；

若f(x)在(0，1)上单调递减，则2x²+2x+a≤0在x∈(0，1)上恒成立；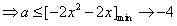

综上，a的取值范围是(-∞，-4]∪[0，+∞)．

(3)(2t-1)²+2(2t-1)+aln(2t-1)≥2t²+4t+2alnt-3恒成立，

a[ln(2t-1)-21nt]≥-2t²+4t-2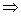a[ln(2t-1)-lnt²]≥2[(2t-1)-t²]，

当t=1时，不等式显然成立；

当t＞1时，t²-(2t-1)=t²-2t+1=(t-1)²＞0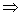t²＞2t-1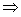lnt²＞ln(2t-1)

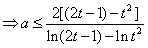在t＞1时恒成立，

令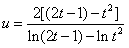，即求u的最小值，

设A(t²，lnt²)，B(2t-1，ln(2t-1))，，

且A、B两点在y=lnx的图象上，

又∵t²＞1，2t-1＞1，

故0＜k_AB＜，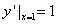

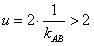∴，故a≤2，

即实数a的取值范围为(-∞，2]。