问题
解答题
已知函数f(x)=-x3+ax2-4，a∈R，
(1)当a=3时，求f(x)在区间[-1，1]上的最大值和最小值；
(2)若存在x0∈(0，+∞)，使得f(x0)＞0，求a的取值范围。
答案
解：(1)当a=3时，
，
，
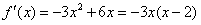当x变化时，f′(x)、f(x)在区间[-1，1]上的变化情况如下表：
所以f(x)在区间[-1，1]上的最大值为f(-1)=0，最小值为f(0)=-4；
(2)
，
若a≤0，则当x∈(0，+∞)时，f′(x)＜0，此时f(x)单调递减，
故f(x)＜f(0)=-4，不存在使题设成立的x0；
若a＞0，则当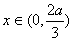
时，f′(x)＞0，此时f(x)单调递增；
当
时，f′(x)＜0，此时f(x)单调递减，
故f(x)在(0，+∞)上的最大值为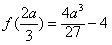
，
所以满足题设的x0存在，当且仅当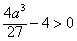
，解得a＞3；
综上，使题设成立的a的取值范围是(3，+∞)。