问题
计算题
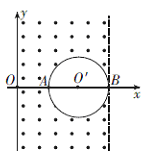
（１８分）如图所示，在ｘｏｙ平面内，有一个圆形区域的直径ＡＢ 与ｘ轴重合，圆心Ｏ′的坐标为（２ａ，０），其半径为ａ，该区域内无磁场． 在ｙ轴和直线ｘ＝３ａ之间的其他区域内存在垂直纸面向外的匀强磁场，磁感应强度大小为Ｂ．一质量为ｍ、电荷量为ｑ的带正电的粒子从ｙ轴上某点射入磁场．不计粒子重力．
（１）若粒子的初速度方向与ｙ轴正向夹角为６０°，且粒子不经过圆形区域就能到达Ｂ点，求粒子的初速度大小ｖ１；
（２）若粒子的初速度方向与ｙ轴正向夹角为６０°，在磁场中运动的时间为Δｔ＝πｍ/３Ｂｑ，且粒子也能到达Ｂ点，求粒子的初速度大小ｖ２；
（３）若粒子的初速度方向与ｙ轴垂直，且粒子从Ｏ′点第一次经过ｘ轴，求粒子的最小初速度ｖｍ．
答案
（1）
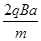；（2）
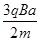；（3）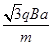
。
题目分析：（1）粒子不经过圆形区域就能达到B点，故粒子到达B点时的速度竖直向下，圆心必在x轴正半轴上，设粒子圆周运动的半径为r1，
由几何关系得：r1sin30°=3a－r1（3分）；又qv1B=m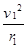
（2分）
解得：v1=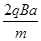（1分）
（2）粒子在磁场中运动的周期T=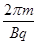
，
故粒子在磁场中的运动轨迹的圆心角为α=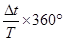
=60°（1分）
粒子到达B点的速度与x轴夹角β=30°（1分）
设粒子做圆周运动的半径为r2由几何关系得：3a=2r2sin30°+2acos230°（3分）
又qv2B=m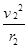
，解得：v2=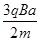（1分）
（3）设粒子从C点进入圆形区域，O′C与O′A夹角为θ，轨迹圆对应的半径为r，由几何关系得：
2a=rsinθ+acosθ（3分）
故当θ=60°时，半径最小为rm=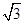
a(2分)
又qvmB=m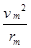
，解得vm=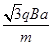(1分)(其他正确解法都给分)