问题
填空题
[2012·安徽高考]设向量a＝(1,2m)，b＝(m＋1,1)，c＝(2，m)．若(a＋c)⊥b，则|a|＝________.
答案
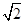
由题意得a＋c＝(3,3m)，由(a＋c)⊥b，可得(a＋c)·b＝0，即3(m＋1)＋3m＝0，解得m＝－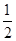
，则a＝(1，－1)，故|a|＝.
搜题请搜索小程序“爱下问搜题”
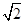[2012·安徽高考]设向量a＝(1,2m)，b＝(m＋1,1)，c＝(2，m)．若(a＋c)⊥b，则|a|＝________.
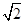
由题意得a＋c＝(3,3m)，由(a＋c)⊥b，可得(a＋c)·b＝0，即3(m＋1)＋3m＝0，解得m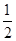＝－，则a＝(1，－1)，故|a|＝.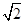