问题
解答题
已知f（x）是二次函数，f′（x）是它的导函数，且对任意的x∈R，f′（x）=f（x+1）+x2恒成立．
（1）求f（x）的解析表达式；
（2）设t＞0，曲线C：y=f（x）在点P（t，f（t））处的切线为l，l与坐标轴围成的三角形面积为S（t）．求S（t）的最小值．
答案
解：（1）设f（x）=ax2+bx+c（其中a≠0），则f'（x）=2ax+b，
f（x+1）=a（x+1）2+b（x+1）+c=ax2+（2a+b）x+a+b+c．
由已知，得2ax+b=（a+1）x2+（2a+b）x+a+b+c，
∴
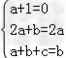，解之，得a=﹣1，b=0，c=1，
∴f（x）=-x2+1．
（2）由（1）得，P（t，1-t2），
切线l的斜率k=f'（t）=-2t，
∴切线l的方程为y-（1-t2）=-2t（x-t），
即y=-2tx+t2+1．
从而l与x轴的交点为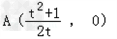
，
l与y轴的交点为B（0，t2+1），
∴
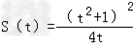（其中t＞0）．
∴
．
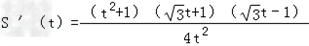当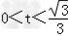
时，S'（t）＜0，S（t）是减函数；
当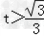
时，S'（t）＞0，S（t）是增函数．
∴
．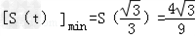