问题
填空题
将编号依次为l,2,3,4的四个同样的小球放进一个不透明的袋子中,摇匀后甲、乙二人做如下游戏:每人从袋子中各摸出一个球,然后将这两个球上的数字相乘,若积为奇数,则甲获胜;若积为偶数,则乙获胜.
请问:在这样的游戏规则下,乙获胜的概率为______.
答案
不妨设甲先摸,则甲、乙所摸得球的情况如下:
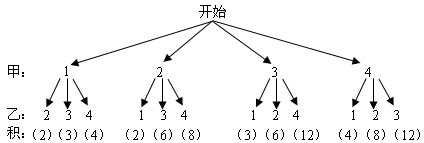
总共有12种情况,每种情况发生的可能性相同,其中积为奇数的情况有2种,积为偶数的情况有10种,所以甲获胜的概率为2÷12=1 6
乙获胜的概率为:10÷12=5 6
答:乙获胜的概率为
;5 6
故答案为:
.5 6
