(16分)电磁感应现象是电磁学中最重大的发现之一,它揭示了电、磁现象之间的本质联系。
电路中感应电动势的大小,跟穿过这一电路的磁通量的变化率成正比,即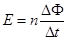 ,这就是法拉第电磁感应定律。
,这就是法拉第电磁感应定律。
(1)如图所示,把矩形线框abcd放在磁感应强度为B的匀强磁场里,线框平面跟磁感线垂直。设线框可动部分ab的长度为L,它以速度v向右匀速运动。请根据法拉第电磁感应定律推导出闭合电路的感应电动势E=BLv。
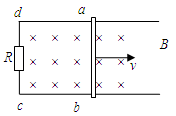
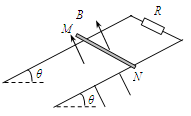
(2)两根足够长的光滑直金属导轨平行放置在倾角为θ的绝缘斜面上,两导轨间距为L。两导轨间接有阻值为R的电阻。一根质量为m的均匀直金属杆MN放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B匀强磁场中,磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆MN由静止沿导轨开始下滑。求
①当导体棒的速度为v(未达到最大速度)时,通过MN棒的电流大小和方向;
②导体棒运动的最大速度。
(1)见解析;(2)①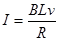 ;电流方向为从N到M;②
;电流方向为从N到M;②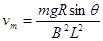 。
。
题目分析:(1)在Δt时间内,ab棒向右移动的距离为vΔt,
这个过程中线框的面积变化量是ΔS=LvΔt (2分)
穿过闭合回路的磁通量的变化量是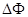 ="BΔS=B" LvΔt (2分)
="BΔS=B" LvΔt (2分)
根据法拉第电磁感应定律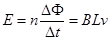 (2分)
(2分)
(2)①当导体棒的速度为v时,产生的感应电动势为E=BLv
回路中的电流大小为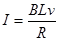 (2分)
(2分)
由右手定则可知电流方向为从N到M (2分)
②导体棒在磁场中运动时,所受安培力大小为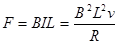 (2分)
(2分)
由左手定则可知,安培力方向沿斜面向上
当导体棒的加速度为零时,速度最大
即: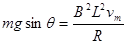 (2分)
(2分)
可解得最大速度为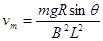 (2分)
(2分)
