问题
计算题
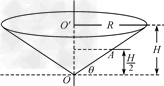
如图所示，一个竖直放置的圆锥筒可绕其中心OO'转动，筒内壁粗糙，筒口半径R＝2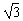
m，筒壁和水平面的夹角θ＝30°，筒内壁A点的高度为筒高的一半．内壁上有一质量为m＝1 kg的小物块放在筒壁上的A处．g取10 m/s2，求：
(1)当筒不转动时，物块静止在筒壁A点受到的摩擦力大小；
(2)当物块在A点随筒做匀速转动，且其受到的摩擦力为零时，筒转动的角速度大小；
(3)若物块与筒壁间的动摩擦因数μ＝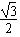
，最大静摩擦力等于滑动摩擦力，要使物块在A点随筒做匀速转动而不产生相对滑动，那么筒转动的最大角速度不能超过多大？
答案
解：(1)f＝mgsinθ
f＝5 N
(2)mgtanθ＝mω2r
r＝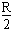
，ω＝
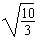rad/s
(3)当角速度最大时筒壁对物块的最大静摩擦力沿筒壁向下
Ncosθ＝fsinθ＋mg
Nsinθ＋fcosθ＝mω2r
f＝μN
ω＝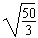
rad/s
最大角速度不能超过ω＝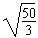
rad/s.