问题
计算题
质量为M、长为
L的杆水平放置，杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳，绳上套着一质量为m的小铁环．已知重力加速度为g.不计空气影响．
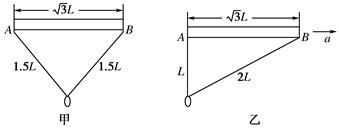
(1)现让杆和环均静止悬挂在空中，如图甲，求绳中拉力的大小；
(2)若杆与环保持相对静止，在空中沿AB方向水平向右做匀加速直线运动，此时环恰好悬于A端的正下方，如图乙所示．
①求此状态下杆的加速度大小a；
②为保持这种状态需在杆上施加一个多大的外力？方向如何？
答案
(1)
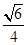mg (2)①
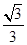g ②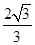
(M＋m)g 方向与水平方向成60°角斜向右上方
正确受力分析，由平衡条件和牛顿第二定律求解．
(1)如图，设平衡时，绳中拉力为FT，有
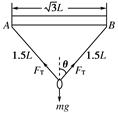
2FTcos θ－mg＝0①
由图知
cos θ＝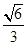
②
由①②式解得
FT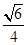＝mg.③
(2)①此时，对小铁环受力分析如图，有
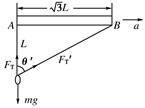
FT′sin θ′＝ma④
FT＋FT′cos θ′－mg＝0⑤
由图知θ′＝60°，代入④⑤式解得
a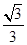＝g.⑥
②如图，设外力F与水平方向成α角，将杆和小铁环当成一个整体，有
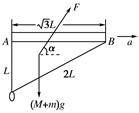
Fcos α＝(M＋m)a⑦
Fsin α－(M＋m)g＝0⑧
由⑥⑦⑧式解得
F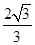＝ (M＋m)g
tan α＝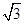
(或α＝60°)．