若存在常数k和b，使得函数f（x）和g（x）在它们的公共定义域上的任意实数x分别满足：
f（x）≥kx+b和g（x）≤kx+b，则称直线l：y=kx+b为函数f（x）和g（x）的“隔离直线”．已知f（x）=x2，g（x）=2elnx．
（I）求F（x）=f（x）﹣g（x）的极值；
（II）函数f（x）和g（x）是否存在隔离直线？若存在，求出此隔离直线的方程，若不存在，请说明理由．
解：（1）∵F（x）=f（x）﹣g（x）=x2﹣2clnx（x＞0），
∴F′（x）=2x﹣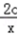
=（2x2﹣2c）/x=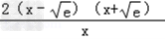
令F′（x）=0，得x= 
，
当0＜x＜ 
时，F′（x）＜0，
X＞ 
时，F′（x）＞0
故当x= 
时，F（x）取到极小值，极小值是0
（2）由（1）可知，函数f（x）和g（x）的图象在x= 
处有公共点，
因此存在f（x）和g（x）的隔离直线，那么该直线过这个公共点，
设隔离直线的斜率为k．则隔离直线方程为y﹣e=k（x﹣
），即y=kx﹣k
+e
由f（x）≥kx﹣
k +e（x∈R），可得x2﹣kx﹣k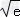
+e，
由f（x）≥kx﹣
k +e（x∈R），可得x2﹣kx+k
﹣e≥0
当x∈R恒成立，则△=k2﹣4k 
+4e=（k﹣2
）2≤0，只有k=2 
，
此时直线方程为：y=2
x﹣e，
下面证明g（x）≤2 
x﹣eexx＞0时恒成立
令G（x）=2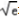
x﹣e﹣g（x）=2 
x﹣e﹣2elnx，
G′（x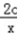）=2 
﹣
=（2 
x﹣2c）/x=2 
（x﹣
）/x，
当x=
时，G′（X）=0，
当0＜x＜ 
时G′（X）＞0，
则当x= 
时，G（x）取到最小值，极小值是0，也是最小值．
所以G（x）=2 
x﹣e﹣g（x）≥0，则g（x）≤2
x﹣e当x＞0时恒成立．
∴函数f（x）和g（x）存在唯一的隔离直线y=2
x﹣e