问题
解答题
已知函数f（x）=axlnx图象上点（e，f（e））处的切线方程与直线y=2x平行（其中e=2.71828…），g（x）=x2﹣tx﹣2．
（I）求函数f（x）的解析式；
（II）求函数f（x）在[n，n+2]（n＞0）上的最小值；
（III）对一切x∈（0，e]，3f（x）≥g（x）恒成立，求实数t的取值范围．
答案
解：（I）由点（e，f（e））处的切线方程与直线2x﹣y=0平行，
得该切线斜率为2，即f'（e）=2．
又∵f'（x）=a（lnx+1），
令a（lne+1）=2，a=1，
所以f（x）=xlnx．
（II）由（I）知f'（x）=lnx+1，
显然f'（x）=0时x=e﹣1
当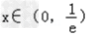
时f'（x）＜0，所以函数
上单调递减．
当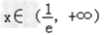
时f'（x）＞0，所以函数f（x）在
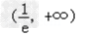上单调递增，
①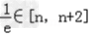
时，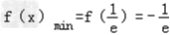
；
②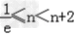
时，函数f（x）在[n，n+2]上单调递增，
因此f（x）min=f（n）=nlnnn；
所以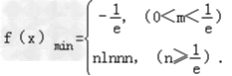
（III）对一切x∈（0，e]，3f（x）≥g（x）恒成立，
又g（x）=x2﹣tx﹣2，
∴3xlnx≥x2﹣tx﹣2，即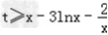
．
设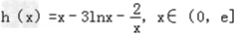
，
则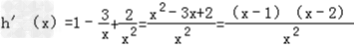
，
由h'（x）=0得x=1或x=2，
∴x∈（0，1），h'（x）＞0，h（x）单调递增，
x∈（1，2），h'（x）＞0，h（x）单调递减，
x∈（2，e），h'（x）＞0，h（x）单调递增，
∴h（x）极大值=h（1）=﹣1，且h（e）=e﹣3﹣2e﹣1＜﹣1，
所以h（x）max=h（1）=﹣1．
因为对一切x∈（0，e]，3f（x）≥g（x）恒成立，
∴t≥h（x）max=﹣1．
故实数t的取值范围为[﹣1，+∞）．