问题
问答题
某机械打桩机原理可简化为如图所示,直角固定杆光滑,杆上套有mA=55kg和mB=80kg两滑块,两滑块用无弹性的轻绳相连,绳长为5m,开始在外力作用下将A滑块向右拉到与水平夹角为37°时静止释放,B滑块随即向下运动带动A滑块向左运动,当运动到绳与竖直方向夹角为37°时,B滑块(重锤)撞击正下方的桩头C,桩头C的质量mC=200kg。碰撞时间极短,碰后A滑块由缓冲减速装置让其立即静止,B滑块反弹上升h1=0.05m,C桩头朝下运动h2=0.2m静止。取g=10m/s2。求:
(1)滑块B碰前的速度;
(2)泥土对桩头C的平均阻力。
答案
⑴3m/s;⑵3280N
设碰前A的速度为V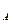 ,B的速度为V
,B的速度为V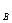 ,由系统机械能守恒定律:
,由系统机械能守恒定律:
m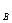 g(Lsin53
g(Lsin53 —Lsin37
—Lsin37 )=
)=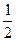 m
m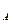 V
V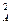 +
+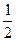 m
m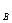 V
V …………………….3分
…………………….3分
物体A和物体B沿绳的分速度相等:
V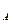 cos53
cos53 =V
=V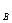 cos37
cos37 ……………………………….. 3分
……………………………….. 3分
联立以上两式得:V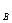 ="3m/s………………………………………." 2分
="3m/s………………………………………." 2分
B与C碰撞动量守恒:m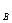 V
V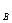 =m
=m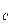 V
V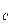 —m
—m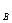 V
V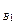 ……………………. 3分.
……………………. 3分.
B碰后竖直上抛:V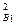 —0=2gh
—0=2gh ………………………………2分
………………………………2分
联立以上两式得:V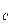 ="1.6m/s…………………………." 2分
="1.6m/s…………………………." 2分
对C用动能定理:mgs—fs=0—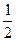 m
m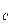 V
V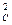 …………………………. 3分
…………………………. 3分
所以f=3280N………………………………2分
