问题
问答题
如图,直角坐标系 中,
中, <O的区域存在沿+
<O的区域存在沿+ 轴方向的匀强电场,场强大小为
轴方向的匀强电场,场强大小为 ,在
,在 >0的区域存在一垂直纸面的矩形有界匀强磁场,其左边界和下边界分别与
>0的区域存在一垂直纸面的矩形有界匀强磁场,其左边界和下边界分别与 、
、 轴重合,磁感应强度大小为
轴重合,磁感应强度大小为 (图中未画出),现有一质量为
(图中未画出),现有一质量为 、电荷量为
、电荷量为 的电子从第二象限的某点P以一定初速度
的电子从第二象限的某点P以一定初速度 (未知)沿+
(未知)沿+ 轴方向开始运动,以
轴方向开始运动,以 的速度经过坐标为(O,L)的Q点,再经过磁场偏转恰好从坐标原点O沿
的速度经过坐标为(O,L)的Q点,再经过磁场偏转恰好从坐标原点O沿 轴的负方向返回电场,求:
轴的负方向返回电场,求:
(1)P点的坐标以及初速度 为多少?
为多少?
(2)矩形磁场区域的最小面积。
答案
(1) 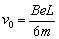 ,
,  ,
,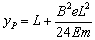 。
。
(2) 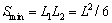 。
。
(1)如图,设P点的坐标为(x,y),从P到Q电子做类平抛运动,经过Q点时速度与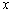 轴正方向的夹角为
轴正方向的夹角为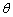 ,
,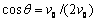 ,
,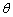 =60°。电子在Q点y轴负方向的分速度
=60°。电子在Q点y轴负方向的分速度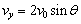 。在电场中电子运动的加速度
。在电场中电子运动的加速度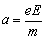 。若电子由P点到Q点的时间为
。若电子由P点到Q点的时间为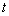 ,则:
,则: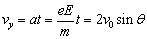 ,所以
,所以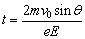 ,
,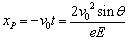 ,
,
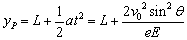 。由题意知,经过磁场偏转恰好从坐标原点O沿
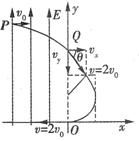
。由题意知,经过磁场偏转恰好从坐标原点O沿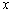 轴的负方向返回电场,说明出电场后并没有直接进入磁场,而是先做直线运动后,才进入磁场(如图),设电子在磁场中做圆周运动的半径为r,则
轴的负方向返回电场,说明出电场后并没有直接进入磁场,而是先做直线运动后,才进入磁场(如图),设电子在磁场中做圆周运动的半径为r,则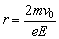 。又
。又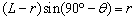 ,所以
,所以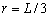 。因此
。因此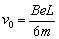 ,代入得
,代入得 ,
,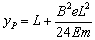 。
。
(2)进入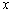 >0的区域后,根据题意,电子开始应做直线运动,然后进入磁场区域,如图所示。设所加最小矩形磁场区域长宽分别为
>0的区域后,根据题意,电子开始应做直线运动,然后进入磁场区域,如图所示。设所加最小矩形磁场区域长宽分别为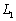 、
、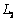 ,
,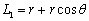 ,
,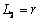 ,
,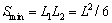 。
。
