问题
问答题
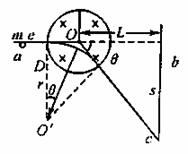
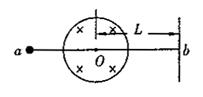
如图所示，有一电子束从点a处以一定的水平速度飞向竖直放置的荧光屏，将垂直击中荧光屏上的点b，已知电子的质量为m，电量为q.
（1）若在电子束运行途中加一半径为R的圆形磁场，磁感应强度为B，方向垂直于纸面向里，圆心O在点a、b连线上，点O距荧光屏距离为L，为使电子束仍击中荧光屏上的点b，可加一个场强为E的匀强电场，指出此匀强电场的方向和范围，并求出电子束的速度．
（2）现撤去电场，电子束以原速度沿原来方向从a点发射，运动方向在磁场中偏转后击中荧光屏上的点c．求b、c间的距离.
答案
（1）电子束的速度v=E/B
（2）b、c间的距离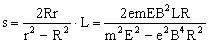
（1）电子进入磁场时受竖直向下的洛伦兹力，要使电子仍击中b点，电子束必须做匀速直线运动，故电子必受竖直向上的电场力。所加电场方向竖直向下，电场的左右边界面与圆O相切。电子受到的合外力为零，可得 evB=eE，v=E/B。
（2）撤去电场后，电子在磁场中由洛伦兹力提供向心力做半径为r的匀速圆周运动，离开磁场区域做匀速直线运动击中屏上点c，如下图所示．
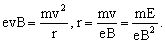
设电子在磁场中偏转的角度为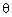
，由直角三角形bOc可得b、c间距离s=Ltan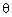．由直角三角形ODO′可得圆形磁场区域半径 
，
。
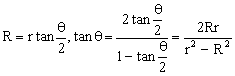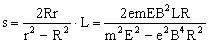