问题
解答题
设函数f（x）=x3﹣ax，x∈R．过图象上一点斜率最小的切线平行于直线x+y=2．
（1）求a的值；
（2）求函数f（x）的单调区间和极值；
（3）已知当x∈（1，+∞）时，f（x）﹣kf（x﹣1）≥0恒成立，求实数k的取值范围．
答案
解：（1）∵f（x）=x3﹣ax，x∈R，
∴f′（x）=3x2﹣a≥﹣a，
∴过图象上一点斜率最小的切线的斜率k=﹣a，
∵过图象上一点斜率最小的切线平行于直线x+y=2，
∴﹣a=﹣1，故a=1．
（2）∵a=1，
∴f（x）=x3﹣x，f′（x）=3x2﹣1，
令f′（x）=3x2﹣1=0，得x= 
列表讨论：
由表讨论知：函数f（x）的单调增区间是 （﹣∞，﹣
）、（
，+∞）；
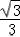单调减区间是（﹣
，
）．极大值f（﹣
）=﹣
+=
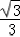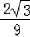，极小值f（
）=
=﹣
．
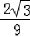（3）∵f（x）﹣kf（x﹣1）≥0，f（x）=x3﹣x，
∴k≤
=
=
=
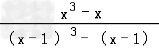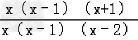=1+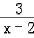
，
∵x∈（1，+∞），当1＜x＜2时，﹣2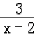＜1+
＜1
当x=﹣2时，1+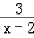
＜+∞，
当x＞2时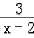，1+
＞1
∴k≤﹣2．