问题
解答题
设函数f（x）=2x3﹣12x+c是定义在R上的奇函数．
（Ⅰ）求c的值及函数f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求函数f（x）的单调递增区间，并求函数f（x）在[﹣1，3]上的最大值和最小值．
答案
解：（Ⅰ）因为f（x）为奇函数，
所以f（﹣x）=﹣f（x）．
即﹣2x3+12x+c=﹣2x3+12x﹣c．
解得c=0．
因为f'（x）=6x2﹣12，
所以切线的斜率k=f'（1）=﹣6．
因为f（1）=﹣10，所以切点为（1，﹣10）．
所以切线方程为y+10=﹣6（x﹣1）．
即6x+y+4=0．
（Ⅱ）由（Ⅰ）知f'（x）=6x2﹣12．
所以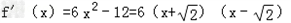
．
列表如下：
所以函数f（x）的单调增区间是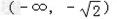
和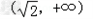
．
因为f（﹣1）=10，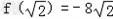
，f（3）=18．
所以f（x）在[﹣1，3]上的最大值是f（3）=18，最小值是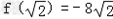
．