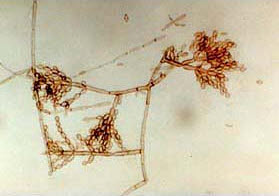
（20分）如图所示，光滑水平地面上方被竖直平面MN分隔成两部分，左边（包括竖直平面MN）有匀强磁场B，右边有匀强电场E0（图中未标）。在O点用长为L＝5m的轻质不可伸长的绝缘细绳系一质量mA＝0.02kg、带负电且电荷量qA＝4×10－4C的小球A，使其在竖直平面内以速度vA＝2.5m/s沿顺时针方向做匀速圆周运动，运动到最低点时与地面刚好不接触。处于原长的轻质弹簧左端固定在墙上，右端与质量mB＝0.01kg、带负电且电荷量qB＝2×10－4C的小球B接触但不连接，此时B球刚好位于M点。现用水平向左的推力将B球缓慢推到P点（弹簧仍在弹性限度内），推力所做的功是W＝2.0J，当撤去推力后，B球沿地面向右运动到M点时对地面的压力刚好为零，继续运动恰好能与A球在最低点发生正碰，并瞬间成为一个整体C（A、B、C都可以看着质点），碰撞前后总电荷量保持不变，碰后瞬间匀强电场大小变为E1＝1×103 N/C，方向不变。g＝10m/s2。求：
（1）匀强磁场的磁感应强度B的大小和方向？
（2）匀强电场的电场强度E0的大小和方向？
（3）整体C运动到最高点时绳对C的拉力F的大小？
（1）B＝25T，方向垂直纸面水平向外
（2）E0＝5×102 N/C，方向竖直向下
（3）F＝1.5N
（1）设B球运动到M点时速度为vB，根据能量守恒有
W＝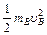
, vB＝20 m / s········································（1分）
B球运动到M点时对地面的压力刚好为零，则
qBvBB＝mBg ·············（1分） 解得B＝25T···············（1分）
B球带负电，受洛伦兹力竖直向上，则磁场方向垂直纸面水平向外。··（1分）
（2）小球A在竖直平面内做匀速圆周运动，所以受到的电场力与重力大小相等、方向相反。即有qAE0＝mAg·····································（1分）
解得E0＝5×102 N/C···········································（1分）
A球带负电，受到的电场力竖直向上，则电场方向竖直向下。·········（1分）
（3）设A、B碰后瞬间整体C带电荷量为qc，质量为mc，速度为vc，由动量守恒
qc＝qA＋qB＝6×10－4C，mc＝mA＋mB＝0.03kg
mBvB－mAvA＝mc vc·············································（1分）
解得vc＝5m/s
设整体C受到电场力和重力的合力为F合，在最低点做圆周运动需要的向心力为F向，则F合＝qcE1－mcg＝0.3N，F向＝
＝0.15N, F合＞F向，所以，细绳将松驰，整体C不会做圆周运动到达最高点，而是从碰后开始做类平抛运动。·························································（2分）
设做类平抛运动的加速度为a，经过时间t在某点S将绳绷紧，对应的水平方向的距离为x，竖直方向的距离为y，如图，则
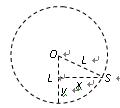
a＝F合/mc····（1分） x＝vct ······（1分）
y＝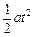
·······························（1分）
且有x2＋(L－y)2＝L2或x2＋(y－L)2＝L2 ····（1分）
解得a＝10 m/s2，t＝1s，x＝5m，y＝5m
由于x＝y＝L，某点S与O点在同一水平位置，C的水平速度变为零。（1分）
C从S点到最高点之间将做圆周运动，设在S点的竖直速度为vs，到达最高点的速度为v，则vs＝at, vs＝10m/s ································（1分）
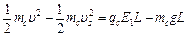, v＝10
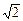m/s·····················（1分）
根据牛顿第二定律得F＋mcg－qcE1＝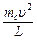
······················（2分）
解得F＝1.5N·················································（1分）
