问题
解答题
已知定义在R上的函数f（x）=x2（ax﹣3），其中a为常数．
（1）若x=1是函数f（x）的一个极值点，求a的值；
（2）若函数f（x）在区间（﹣1，0）上是增函数，求a的取值范围；
（3）若函数g（x）=f（x）+f'（x），x∈0，2]，在x=0处取得最大值，求正数a的取值范围．
答案
解：（1）∵f（x）=ax3﹣3x2
∴f'（x）=3ax2﹣6x=3x（ax﹣2）．
∵x=1是f（x）的一个极值点，
∴f'（1）=0， ∴a=2
（2）①当a=0时 f（x）=﹣3x2在区间（﹣1，0）上是增函数 ∴a=0符合题意；
②当a≠0时，f'（x）=3ax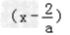
，令f'（x）=0得：x1=0，x2= 
当a＞0时，对任意x∈（﹣1，0），f'（x）＞0， ∴a＞0 （符合题意）
当a＜0时，当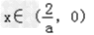
时f'（x）＞0， ∴ 
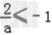，∴﹣2≤a＜0（符合题意）
综上所述，a≥﹣2．
（3）a＞0，g（x）=ax3+（3a﹣3）x2﹣6x，x∈[0，2]．
g'（x）=3ax2+2（3a﹣3）x﹣6=3[ax2+2（a﹣1）x﹣2]，
令g'（x）=0，即ax2+2（a﹣1）x﹣2=0（*），显然有△=4a2+4＞0．
设方程（*）的两个根为x1，x2，由（*）式得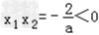 
，
不妨设x1＜0＜x2．
当0＜x2＜2时，g（x2）为极小值
所以g（x）在[0，2]上的最大值只能为g（0）或g（2）
当x2≥2时，由于g（x）在[0，2]上是单调递减函数
所以最大值为g（0），所以在[0，2]上的最大值只能为g（0）或g（2）
又已知g（x）在x=0处取得最大值
所以g（0）≥g（2）即0≥20a﹣24，解得a≤
，
又因为a＞0，所以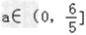
．
故答案为：（1）a=2；（2）a≥﹣2；（3） 
