问题
解答题
已知函数f(x)=x3+ax2+bx+c的图象经过原点,f′(1)=0,
曲线y=f(x)在原点处的切线到直线y=2x+3的角为135°.
(1)求f(x)的解析式;
(2)若对于任意实数α和β,不等式|f(2sinα)﹣f(2sinβ)|≤m恒成立,求m的最小值.
答案
解:(1)由题意有f(0)=c=0,f'(x)=3x2+2ax+b
且f′(1)=3+2a+b=0
又曲线y=f(x)在原点处的切线的斜率k=f′(0)=b,
而直线y=2x+3到此切线所成的角为135°,
所以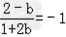 ②
②
联立①②解得a=0,b=﹣3
∴f(x)=x3﹣3x
(2)|f(2sinα)﹣f(2sinβ)|≤m恒成立
等价于|f(x)max﹣f(x)min|≤m
由于2sinα∈[﹣2,2],2sinβ∈[﹣2,2],
故只需求出f(x)=x3﹣3x在[﹣2,2]上的最值,
而f′(x)=3x2﹣3,
由f′(x)=0得x=±1
列表如下:

∴f(x)max=2,f(x)min=﹣2
∴f(x)max﹣f(x)min|=4≤m
∴m的最小值为4
