问题
填空题
如图所示的正方形的盒子开有a、b、c三个微孔盒内有垂直纸面向里的匀强磁场.一束速率不同的电子从a孔沿垂直磁感线方向射入盒中,发现从c孔和b孔有电子射出,则

(1)从b孔和c孔射出的电子的速率之比vb:vc为 .
(2)从b孔和c孔射出的电子在盒内运动时间之比为 .
答案
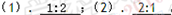
电子垂直射入匀强磁场中,由洛伦兹力提供向心力,做匀速圆周运动.根据牛顿第二定律推导出电子圆周运动的速率与半径的关系.根据几何知识确定电子从c孔和b孔时半径关系,求解速率之比.根据时间与周期的关系,求解时间之比.
解:(1)设电子的质量为m,电量为q,磁感应强度为B,电子圆周运动的半径为r,速率为v,则有qvB=m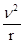 ,得到,v=
,得到,v=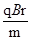 ,r与v成正比.由图看出,从b孔和c孔射出的电子半径之比rb:rc=1:2,则速率之比vb:vc=rb:rc=1:2.
,r与v成正比.由图看出,从b孔和c孔射出的电子半径之比rb:rc=1:2,则速率之比vb:vc=rb:rc=1:2.
(2)电子圆周运动的周期为T=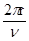 ,又v=
,又v=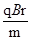 ,得到T=
,得到T=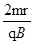 ,可见周期不变.从b孔和c孔射出的电子在盒内运动时间分别为tb=
,可见周期不变.从b孔和c孔射出的电子在盒内运动时间分别为tb=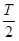 ,tc=
,tc=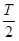 ,所以从b孔和c孔射出的电子在盒内运动时间之比为tb:tc=2:1.
,所以从b孔和c孔射出的电子在盒内运动时间之比为tb:tc=2:1.
点评:本题是带电粒子在磁场中圆周运动的轨迹问题,是磁场、圆周运动及几何知识的综合应用.
