问题
解答题
已知f（x）=lnx+x2﹣bx．
（1）若函数f（x）在其定义域内是增函数，求b的取值范围；
（2）当b=﹣1时，设g（x）=f（x）﹣2x2，求证函数g（x）只有一个零点．
答案
（1）解：∵f（x）在（0，+∞）上递增，
∴f'（x）=
+2x﹣b≥0，对x∈（0，+∞）恒成立，即b≤
+2x对x∈（0，+∞）恒成立，
∴只需b≤（
+2x）min（x＞0），
∵x＞0，
∴
+2x≥2
，当且仅当x=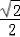
时取“=”，
∴b≤2
，
∴b的取值范围为（﹣∞，2
]．
（2）证明：当b=﹣1时，g（x）=f（x）﹣2x2=lnx﹣x2+x，其定义域是（0，+∞），
∴g'（x）=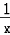
﹣2x+1=﹣
，
令g'（x）=0，
∵x＞0，∴x=1，
当0＜x＜1时，g'（x）＞0；
当x＞1时，g'（x）＜0，
∴函数g（x）在区间（0，1）上单调递增，在区间（1，+∞）上单调递减，
∴当x≠1时，g（x）＜g（1），即g（x）＜0，
当x=1时，g（x）=0．
∴函数g（x）只有一个零点．