问题
解答题
己知f（x）=Inx﹣ax2﹣bx．
（Ⅰ）若a=﹣1，函数f（x）在其定义域内是增函数，求b的取值范围；
（Ⅱ）当a=1，b=﹣1时，证明函数f（x）只有一个零点；
（Ⅲ）f（x）的图象与x轴交于A（x1，0），B（x2，0），两点，AB中点为C（x0，0），求证：f'（x0）＜0．
答案
解：（Ⅰ）依题意：f（x）=lnx+x2﹣bx f（x）在（0，+∞）上递增，
∴
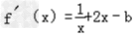≥0对x∈（0，+∞）恒成立
即
对x∈（0，+∞）恒成立，
只需
∵x＞0，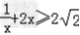 
当且仅当
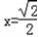时取=
∴
∴b的取值范围为 
（Ⅱ）当a=1，b=﹣1时，f（x）=lnx﹣x2+x，其定义域是（0，+∞）
∴
= 
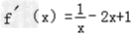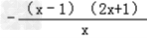
∴0＜x＜1时，f′（x）＞0当x＞1时，f′（x）＜0
∴函数f（x）在区间（0，1）上单调递增，在区间（1，+∞）上单调递减
∴当x=1时，函数f（x）取得最大值，其值为f（1）=ln1﹣1+1=0
当x≠1时，f（x）＜f（1）=0
∴函数f（x）只有一个零点
（Ⅲ）由已知得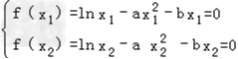
两式相减，
得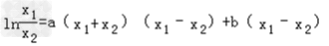
由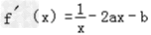 
及2x0=x1+x2，得
=
=
=
= 
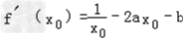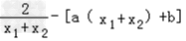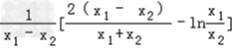令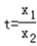
∈（0，1）且 
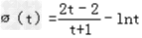（0＜t＜1）
∴
∴
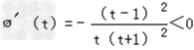
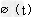在（0，1）上递减，
∴
＞
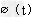=0
x1＜x2，f′（x0）＜0