问题
计算题
在现代科技中,人们常常利用电场、磁场和重力场来控制带电微粒的运动。如图所示,直角坐标系位于竖直面内,y轴上的A点有一带正电的小球,小球的质量为m、电量为q, 。若将小球从A点由静止释放,小球在场强为E1、方向平行于坐标平面的匀强电场和重力场的作用下沿直线做匀加速运动到X轴上的B点。在X轴的上方,小球在场强为E2、磁感应强度为B=
。若将小球从A点由静止释放,小球在场强为E1、方向平行于坐标平面的匀强电场和重力场的作用下沿直线做匀加速运动到X轴上的B点。在X轴的上方,小球在场强为E2、磁感应强度为B= T的磁场和重力场作用下做匀速圆周运动,轨迹是圆周的一部分,且关于y轴对称,已知A、B两点坐标分别为A(0,-l),B(
T的磁场和重力场作用下做匀速圆周运动,轨迹是圆周的一部分,且关于y轴对称,已知A、B两点坐标分别为A(0,-l),B( ,0),g取10m/s2,求:
,0),g取10m/s2,求:
(1)场强E2的大小和方向;
(2)场强E1的大小和方向。(结果可以保留根式)

答案
解:(1)粒子在x轴上方做匀速圆周运动,所以洛伦兹力充当向心力,电场力和重力平衡

解得E2=10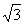 N/C,方向竖直向上
N/C,方向竖直向上
(2)在△AOB中,∠ABO=30°,半径O1B与x轴成60°,所以Rcos60°=OB
解得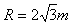
根据牛顿第二定律,粒子做圆周运动时有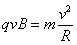
解得: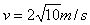
从A到B做匀加速直线运动,则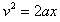
解得a=10m/s2
根据平行四边形定则,有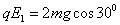
解得E1=30N/C,与x轴正方向成60°斜向上
