问题
计算题
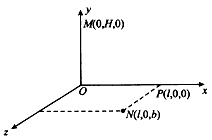
如图所示,Oxyz坐标系的y轴竖直向上,坐标系所在的空间存在匀强电场和匀强磁场,电场方向与x轴平行,从y轴上的M(0、H、0)点无初速释放一个质量为m、电荷量为q的带正电的小球,它落在xOy平面上的N(l、0、b)点(l>0, b>0)。若撤去磁场则小球落在xoz平面的P(l、0、b)点,已知重力加速度为g。
(1)已知磁场方向与某个坐标轴平行,请确定其可能的具体方向;
(2)求出电场强度的大小;
(3)求出小球落至N点时的速率。
答案
解:(1)用左手定则判断出:磁场方向为x方向或y 方向
(2)在未加匀强磁场时,带电小球在电场力和重力作用下落到P点,设运动时间为t,小球自由下落,有H=gt2/2
小球沿x轴方向只受电场力作用,F=qE
小球沿x轴的位移为l=at2/2
小球沿x轴方向的加速度为a=F/m
联立求解,得E=mgl/qH
(3)带电小球在匀强磁场和匀强电场共存的区域运动时,洛伦兹力不做功,
电场力做功为:W=qEl
重力做功为WC=mgH
设落到N点时速度大小为v,根据动能定理得
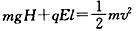
解得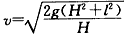 。
。
