问题
解答题
已知P（x，y）为函数y=lnx图象上一点，O为坐标原点，记直线OP的斜率为k=f（x）．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）求函数F（x）=x﹣f（x）的最小值．
答案
解：（Ⅰ）k=f（x）=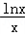
（x＞0），
求导函数可得f′（x）=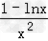
令f′（x）＞0，x＞0，可得0＜x＜e；
令f′（x）＜0，可得x＞e
∴f（x）在（0，e）单调递增，（e，+∞）单调递减．
（Ⅱ）F（x）=x﹣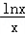
，求导函数可得F′（x）=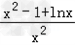
设h（x）=x2﹣1+lnx，求导函数可得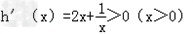
∴h（x）在（0，+∞）为单调递增函数．
∵h（1）=0，∴F'（1）=0，除了1之外，F（x）无其他零点，
∴当x=1时，F（1）=1为最小值．