问题
计算题
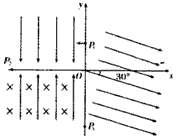
如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第二象限内,有一个竖直向下的匀强电场;在第三象限,存在沿y轴正方向的匀强电场和垂直xOy平面(纸面)向里的匀强磁场;在第一、第四象限,存在着与x轴正方向夹角为30°的匀强电场,四个象限的电场强度大小均相等。一质量为m、电量为+q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限,然后经过x轴上x=-2h处的P2的进入第三象限,带电质点恰好能做匀速圆周运动,之后经过y轴上y=-2h处的P3点进入第四象限,已知重力加速为g。求:
(1)粒子到达P2点时速度的大小和方向;
(2)电场强度和磁感应强度的大小;
(3)带电质点在进入第四象限空间运动过程中离x轴最小距离。
答案
解:(1)设第三象限的电场强度大小为E,由粒子进入第三象限恰好能做匀速圆周运动知:
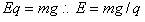
在第二象限,竖直方向加速度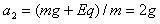
∴水平方向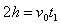 ,竖直方向
,竖直方向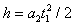
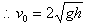 ,
,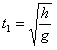
竖直方向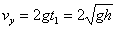
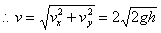
与x轴负向夹角θ,则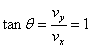
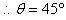
(2)进入第三象限重力和电场力抵消,磁场力提供向心力,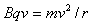
解得: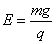 ,
,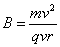
(3)粒子进入第四象限竖直向下的力大小
竖直向下加速度大小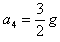
当粒子竖直向上的速度为0时,离x轴最近
即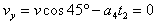
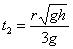
∴粒子上升的最大高度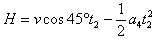
∴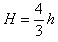
∴离x轴最近的距离