问题
问答题
在天体运动中，将两颗彼此距离较近，且相互绕行的行星称为双星。已知两行星质量分别为M1和M2，它们之间距离为L，求各自运转半径和角速度为多少？
答案
=
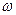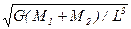
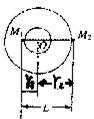在本题中，双星之间有相互吸引力而保持距离不变，则这两行星一定绕着两物体连线上某点做匀速圆周运动，设该点为O，如图所示，M1OM2始终在一直线上，M1和M2的角速度相等，其间的引力充当向心力
解答：引力大小为
F=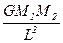
引力提供双星做圆周运动的向心力
F=M1r1w2
= M2r2w2
而
r1+r2=L
由此即可求得
r1=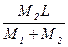
r2=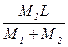
=
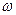