问题
计算题
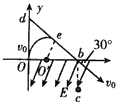
一质量为m、带电量为+q的粒子以速度v0从O点沿y轴正方向射入一圆形匀强磁场区域,磁场方向垂直纸面向外,粒子飞出磁场区域后,从b处穿过x 轴,速度方向与x轴正方向的夹角为30°,同时进入场强大小为大小为E,方向沿x轴负方向成60°角斜向下的匀强电场中,通过了b点正下方c点,如图所示。已知b到O的距离为L,粒子的重力不计,试求:
(1)磁感应强度B;
(2)圆形匀强磁场区域的最小面积;
(3)c点到b点的距离。

答案
解:(1)粒子在磁场中受洛伦兹力作用,做匀速圆周运动,设其半径为R,据此并由题意知,粒子在磁场中的轨迹的圆心O'必在x轴上,且b点在磁场区之外,过b沿速度方向作延长线,它与y轴相交于d点,作圆弧过O点与y轴相切,并且与bd相切,切点e即粒子离开磁场区的地点。这样可求得圆弧轨迹的圆心O',如图所示:
由图中几何关系得:L=3R ①
洛伦兹力提供向心力
由①②求得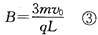
(2)要使磁场的区域有最小面积,则Oe应为磁场区域的直径,由几何关系知: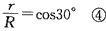
由①④得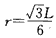
∴匀强磁场的最小面积为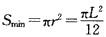
(3)带电粒子进入电场后,由于速度方向与电场力方向垂直,故做类平抛运动,由运动的合成知识有:
s·sin30°=V0t
s·cos30°=at2/2
而a=qE/m
联立解得