问题
解答题
已知函数f（x）=x3+3ax2+（3﹣6a）x+12a﹣4（a∈R）
（Ⅰ）证明：曲线y=f（x）在x=0的切线过点（2，2）；
（Ⅱ）若f（x）在x=x0处取得最小值，x0∈（1，3），求a的取值范围．
答案
解：（Ⅰ）f'（x）=3x2+6ax+3﹣6a
由f（0）=12a﹣4，f'（0）=3﹣6a，
可得曲线y=f（x）在x=0处的切线方程为y=（3﹣6a）x+12a﹣4，
当x=2时，y=2（3﹣6a）+12a﹣4=2，可得点（2，2）在切线上
∴曲线y=f（x）在x=0的切线过点（2，2）
（Ⅱ）由f'（x）=0得 x2+2ax+1﹣2a=0…（1）
方程（1）的根的判别式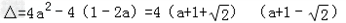
①当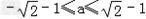
时，函数f（x）没有极小值
②当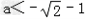
或
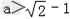时，由f'（x）=0得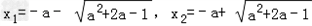
故x0=x2，由题设可知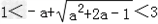
（i）当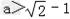
时，不等式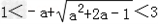
没有实数解；
（ii）当
时，不等式
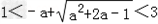化为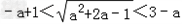
，
解得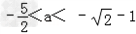
综合①②，得a的取值范围是