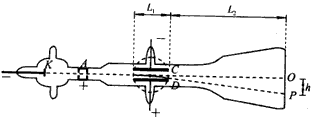
1897年汤姆生通过对阴极射线的研究,发现了电子,从而使人们认识到原子是可分的。汤姆生当年用来测定电子比荷(电荷量e与质量m之比)的实验装置如图所示,真空玻璃管内C、D为平行板电容器的两极,圆形阴影区域内可由管外电磁铁产生一垂直纸面的匀强磁场,圆形区域的圆心位于C、D中心线的中点,直径与C、D的长度相等,已知极板C、D的长度为L1,C、D间的距离为d,极板右端到荧光屏的距离为L2。由K发出的电子,经A与K之间的高电压加速后,形成一束很细的电子流,电子流沿C、D中心线进入板间区域,若C、D间无电压,则电子将打在荧光屏上的O点;若在C、D间加上电压U,则电子将打在荧光屏上的P点,P点到O点的距离为h;若再在圆形区域内加一方向垂直于纸面向外、磁感应强度为B的匀强磁场,则电子又打在荧光屏上的O点。不计重力影响。
(1)求电子打在荧光屏O点时速度的大小;
(2)推导出电子比荷的表达式;
(3)利用这个装置,还可以采取什么方法测量电子的比荷?
解:(1)加上磁场后,电子所受电场力与洛伦兹力相等,电子做匀速直线运动,则
evB=eE
又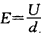
即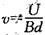
(2)若在两极板间加上电压U,电子在水平方向做匀速运动,通过极板所需的时间为
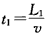
电子在竖直方向做匀加速运动,加速度为
在时间t1内垂直于极板方向竖直向下偏转的距离为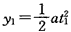
离开极板区域时竖直向下的分速度为vy=at1
电子离开极板区域后做匀速直线运动,经t2时间到达荧光屏,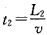
在时间t2内向下运动的距离为y2=vyt2
则h=y1+y2
解得:
(3)说出任何一种合理方法均可,例如:
①测量出A与K之间的电压U';再在两极板间加上电压U,电子将打在荧光屏上的P点;测出OP的长度便能计算电子的比荷;
②测量出A与K之间的电压U';只在圆形区域内加一方向垂直于纸面的磁感应强度为B的匀强磁场,电子将打在荧光屏上的P'点;测出OP'的长度便能计算电子的比荷;
③在两极板间加上电压U,在圆形区域内加一方向垂直于纸面的磁感应强度为B的匀强磁场,使电子打在荧光屏上的O点;再撤去两极板间加上电压,电子将打在荧光屏上的P'点;测出OP'的长度便能计算电子的比荷;
④只在两极板间加上电压U,电子将打在荧光屏上的P点;只在圆形区域内加一方向垂直于纸面的磁感应强度为B的匀强磁场,电子将打在荧光屏上的P'点;测出OP、OP'的长度便能计算电子的比荷。
