问题
计算题
如图所示,在 的空间有垂直纸面向里的匀强磁场,磁感应强度B=4×10-3T,在y≤0空间同时存在沿y轴负方向的匀强电场,电场强度
的空间有垂直纸面向里的匀强磁场,磁感应强度B=4×10-3T,在y≤0空间同时存在沿y轴负方向的匀强电场,电场强度 一个质量m=6.4×10-27kg带电量q=+3.2×10-19C的带电粒子以初速度v0=2×l04m/s从y轴上的P点(纵坐标为
一个质量m=6.4×10-27kg带电量q=+3.2×10-19C的带电粒子以初速度v0=2×l04m/s从y轴上的P点(纵坐标为 )出发,沿着-y方向进入区域I。粒子重力不计,粒子在整个运动过程中始终没有穿出电磁场区域。
)出发,沿着-y方向进入区域I。粒子重力不计,粒子在整个运动过程中始终没有穿出电磁场区域。
(1)求带电粒子第一次穿越x轴时的横坐标x;
(2)请结合运动合成和分解的知识,求出带电粒子在区域Ⅱ中到达最低点的纵坐标y。
(3)求带电粒子从进入区域I开始到第二次穿越x轴时经过的时间t。

答案
解:(1)由 得
得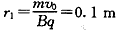
由图中几何关系可知:
即带电粒子离开区域I时的速度方向与x轴正向成300角
所以,带电粒子第一次通过x轴时的坐标x=r1-r1cos600=0.05m
(2)将带电粒子进入区域Ⅱ时的速度沿坐标轴分解,
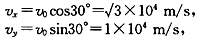
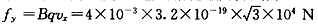
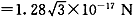
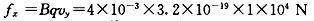
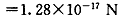
可见,fy=F,二力平衡
所以,带电粒子在区域Ⅱ中的运动,可视为沿x轴正向的速度为vx的匀速直线运动和以速率为vy、洛伦兹力Bqvy作为向心力的匀速圆周运动的叠加,
轨迹如图所示,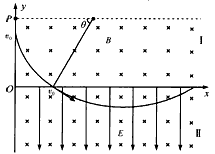
圆周运动半径为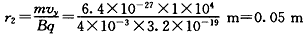
粒子做匀速圆周运动四分之一周期后,到达最低点,对应的纵坐标y= -r2=-0. 05m
(3)粒子做匀速圆周运动,
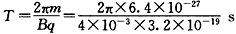
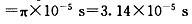
带电粒子从进入区域l开始到第一次芽越x轴,经过的时间t1=T/6
粒子在区域Ⅱ中做匀速圆周运动半个周期后,第二次穿越x轴,经历时间t2=T/2
故带电粒子从进入区域I开始到第二次穿越z轴时经过的时间
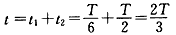
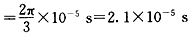 。
。
