问题
计算题
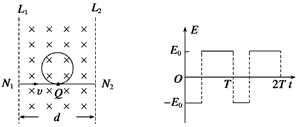
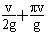如图甲所示，宽度为d的竖直狭长区域内（边界为L1、L2），存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场（如图乙所示），电场强度的大小为E0，E>0表示电场方向竖直向上。t＝0时，一带正电、质量为m的尘埃从左边界上的N1点以水平速度v射入该区域，沿直线运动到Q点后，做一次完整的圆周运动，再沿直线运动到右边界上的N2点。Q为线段N1N2的中点，重力加速度为g。上述d、E0、m、v、g为已知量。
（1）求微粒所带电荷量q和磁感应强度B的大小；
（2）求电场变化的周期T；
（3）改变宽度d，使微粒仍能按上述运动过程通过相应宽度的区域，求T的最小值。
答案
解：（1）微粒做匀速圆周运动说明其重力和电场力平衡，即mg＝qE0
故微粒所带电荷量q＝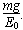
由于粒子在刚开始和最后一段做直线运动，对其受力分析如图所示，则qvB＝qE0＋mg
则B＝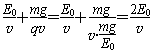
（2）经分析从N1点到Q点粒子做匀速直线运动的时间t1＝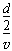
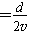
到Q点后做匀速圆周运动的周期T′＝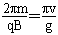
从Q点到N2点粒子做匀速直线运动，其运动时间t2＝t1
则由题中图象可知电场变化的周期T＝t1＋T′＝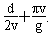
（3）改变宽度d时，仍能完成上述运动过程的电场变化的最小周期的对应示意图如图所示（“略”）
则Tmin＝t1′＋T′
此时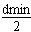
＝R
则t1′＝
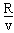且R＝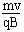
以上各式联立解得Tmin＝