问题
解答题
已知函数f（x）=ax+lnx（a∈R）．
（Ⅰ）若a=2，求曲线y=f（x）在x=1处切线的斜率；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=x2﹣2x+2，若对任意x1∈（0，+∞），均存在x2∈[0，1]，使得f（x1）＜g（
x2），求a的取值范围．
答案
解：（Ⅰ）由已知
，则f'（1）=2+1=3．
故曲线y=f（x）在x=1处切线的斜率为3；
（Ⅱ）
．
①当a≥0时，由于x＞0，故ax+1＞0，f'（x）＞0
所以，f（x）的单调递增区间为（0，+∞）．
②当a＜0时，由f'（x）=0，得
．
在区间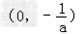
上，f'（x）＞0，
在区间
上f'（x）＜0，
所以，函数f（x）的单调递增区间为
，单调递减区间为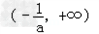
；
（Ⅲ）由已知，转化为f（x）max＜g（x）min．
由x∈[0，1]，得到g（x）min=g（1）=1，
由（Ⅱ）知，当a≥0时，f（x）在（0，+∞）上单调递增，值域为R，故不符合题意．
当a＜0时，f（x）在
上单调递增，在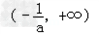
上单调递减，
故f（x）的极大值即为最大值，
，
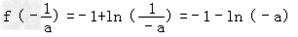所以1＜﹣1﹣ln（﹣a），解得
．