（10分）某飞船升空后，进入近地点距地心为r1，远地点距地心为r2的椭圆轨道正常运行，然后飞船推进舱发动机点火，飞船开始变轨，即飞船在远地点时，将质量为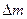
的燃气以一定的速度向后方喷出后，飞船改做半径为r2的圆周运动。设距地球无穷远处为引力势能零点，则距地心为r、质量为
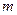的物体的引力势能表达式为
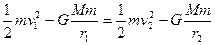。已知地球质量
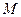，万有引力常量G，地球表面处重力加速度为g，飞船总质量为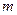，飞船沿椭圆轨道正常运行时远地点、近地点两处的速率与距地心的距离乘积相等。求：
（1）地球半径；
（2
）飞船在远地点的速度大小v2 ；
（3）飞船在远地点时，应将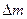的气体相对于地
球多大的速度向后方喷出才能进入半径为r2的圆轨道。
（1）
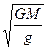（2）
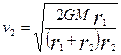（3）
(1)地面附近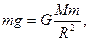 
...................（1分）
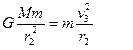
R=" " 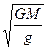……………………… （1分）
(2)由开普勒
第二定律得 
v1 r1= v2 r2 ……………………… （1分） 
飞船在椭圆轨道上运行，机械能守恒
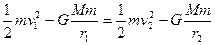……………………（1分）
则联立得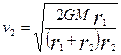 ………………（1分） (3)设飞船在圆轨道上运行的速度为v3，则
.................（1分）
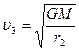……………………………（1分）
由动量守恒定律得 mv2=(m-Δm)v3 -Δmv0 ..................（1分） 
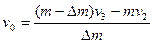………………………（1分）
得 …………（1分）