问题
计算题
如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场, 宽度为d,两侧为相同的匀强磁场,方向垂直纸面向里,一质量为m、带电量+q、重力不计的带电粒子,以初速度v1垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动, 已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推求 (1)粒子第一次经过电场的过程中电场力所做的功W1;
(2)粒子第n次经过电场时电场强度的大小En;
(3)粒子第n次经过电场所用的时间tn;
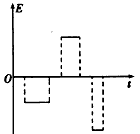
(4)假设粒子在磁场中运动时,电场区域场强为零,请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标刻度值)

答案
解:(1)设磁场的磁感应强度大小为B,粒子第n次进入磁场时的半径为Rn,速度为vn,
由牛顿第二定律得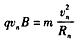 ①
①
由①得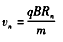 ②
②
因为R2=2R1,所以v2=2v1 ③
对于粒子第一次在电场中的运动,由动能定理得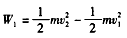 ④
④
联立③④得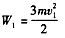 ⑤
⑤
(2)粒子第n次进入电场时速度为vn,出电场时速度为vn+1,有vn=nv1,vn+1=(n+1)v1 ⑥
由动能定理得 ⑦
⑦
(3)设粒子第n次在电场中运动的加速度为an,由牛顿第二定律得qEn=man ⑨
由运动学公式得vn+1-vn= antn⑩
(4)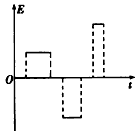 或
或