问题
解答题
已知函数f（x）=ax3+x2+bx（其中常数a，b∈R），g（x）=f（x）+f'（x）是奇函数．
（1）求f（x）的表达式；
（2）讨论g（x）的单调性，并求g（x）在区间[1，2]上的最大值和最小值．
答案
解：（1）由题意得f'（x）=3ax2+2x+b
因此g（x）=f（x）+f'（x）=ax3+（3a+1）x2+（b+2）x+b
因为函数g（x）是奇函数，所以g（﹣x）=﹣g（x），
即对任意实数x，
有a（﹣x）3+（3a+1）（﹣x）2+（b+2）（﹣x）+b=﹣[ax3+（3a+1）x2+（b+2）x+b]
从而3a+1=0，b=0， 解得
，
因此f（x）的解析表达式为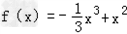
．
（2）由（1）知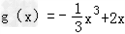
， 所以g'（x）=﹣x2+2，
令g'（x）=0 解得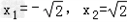
则当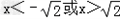
时，g'（x）＜0
从而g（x）在区间
，
上是减函数，
当
，
从而g（x）在区间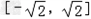
上是增函数，
由前面讨论知，g（x）在区间[1，2]上的最大值与最小值只能在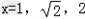
时取得，
而
，
因此g（x）在区间[1，2]上的最大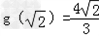值为
，最小值为
．