问题
计算题
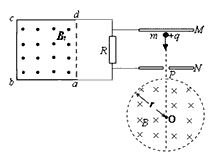
如图所示,串联阻值为R的闭合电路中,面积为S的正方形区域abcd存在一个方向垂直纸面向外、磁感应强度均匀增加且变化率为k的匀强磁场Bt,abcd的电阻值也为R,其他电阻不计。电阻两端又向右并联一个平行板电容器。在靠近M板处由静止释放一质量为m、电量为+q的带电粒子(不计重力),经过N板的小孔P进入一个垂直纸面向内、磁感应强度为B的圆形匀强磁场,已知该圆形匀强磁场的半径为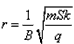 。求:
。求:
(1)电容器获得的电压;
(2)带电粒子从小孔P射入匀强磁场时的速度;
(3)带电粒子在圆形磁场运动时的轨道半径及它离开磁场时的偏转角。
答案
解:(1)根据法拉第电磁感应定律,闭合电路的电动势为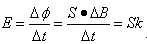
根据闭合电路的欧姆定律,闭合电路的电流为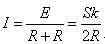
电阻获得的电压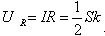
因电容器与电阻是并联的,故电容器获得的电压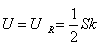
(2)带电粒子在电容器中受到电场力作用而做匀加速直线运动,根据动能定理,有: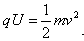
得到带电粒子从小孔射入匀强磁场时的速度为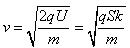
(3)带电粒子进入圆形匀强磁场后,洛伦兹力提供其做匀速圆周运动的向心力,有: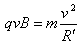
得带电粒子在圆形匀强磁场运动的半径为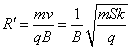
又圆形磁场的半径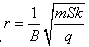 ,即
,即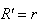
根据左手定则,带电粒子在圆形磁场向右转过的圆周(如右图所示),故它离开磁场时的偏转角为90°。
