解：由题设知k≠0且f'（x）=3kx（x﹣2）

0＜x＜2时，x（x﹣2）＜0；

x＜0或x＞2时，x（x﹣2）＞0；

x=0和x=2时，f'（x）=0．

由题设知﹣2≤x≤2，f（﹣2）=﹣20k+b，f（0）=b，f（2）=﹣4k+b

①k＜0时，﹣2＜x＜0时，f'（x）＜0；0＜x＜2时，f'（x）＞0，

∴f（x）在（﹣2，0）上单减，在（﹣2，2）和上单增，

x=0为f（x）的极小值点，也是最小值点；

∵f（﹣2）＞f（2）

∴f（x）的最大值是f（﹣2）

解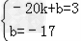，解得k=﹣1，b=﹣17

②k＞0时，﹣2＜x＜0时，f'（x）＞0；0＜x＜2时，f'（x）＜0，

∴f（x）在（﹣2，0）上单增，在（﹣2，2）和上单减

x=0为f（x）的极大值点，也是最大值点；

∵f（﹣2）＜f（2）

∴f（x）的最小值是f（﹣2）

解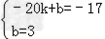，解得k=1，b=3

综上，k=﹣1，b=﹣17或k=1，b=3