问题
计算题
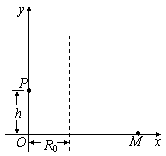
如图,空间存在匀强电场和匀强磁场,电场方向为y轴正方向,磁场方向垂直于xy平面(纸面)向外,电场和磁场都可以随意加上或撤除,重新加上的电场或磁场与撤除前的一样。一带正电荷的粒子从P(x=0,y=h)点以一定的速度平行于x轴正方向入射。这时若只有磁场,粒子将做半径为R0的圆周运动;若同时存在电场和磁场,粒子恰好做直线运动。现在,只加电场,当粒子从P点运动到x=R0平面(图中虚线所示)时,立即撤除电场同时加上磁场,粒子继续运动,其轨迹与x轴交于M点,不计重力。已知h=6cm,R0=10cm,求:
(1)粒子到达x=R0平面时速度方向与x轴的夹角以及粒子到x轴的距离;
(2)M点的横坐标xM。
答案
解:(1)做直线运动有: ①
①
做圆周运动有: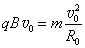 ②
②
只有电场时,粒子做类平抛运动,有: ③
③
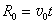 ④
④
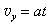 ⑤
⑤
从③④⑤解得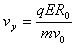 ⑥,从①得E=Bv0 ⑦,从②式得
⑥,从①得E=Bv0 ⑦,从②式得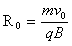 ⑧,将⑦、⑧代入⑥得:
⑧,将⑦、⑧代入⑥得: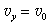
粒子速度大小为: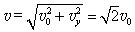
速度方向与x轴夹角为: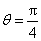
粒子与x轴的距离为: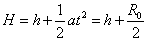
代入数据得H=11cm
(2)撤电场加上磁场后,有: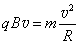
解得: ,代入数据得
,代入数据得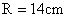
粒子运动轨迹如图所示,圆心C位于与速度v方向垂直的直线上,该直线与x轴和y轴的夹角均为π/4

由几何关系得C点坐标为: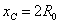 ,代入数据得
,代入数据得
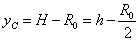 ,代入数据得
,代入数据得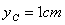
过C作x轴的垂线,在ΔCDM中: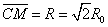 ,
,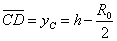
解得: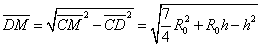
M点横坐标为: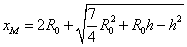
代入数据得
