解：（1）函数f（x）=e^x-ax-2的定义域是R，f′（x）=e^x-a，

若a≤0，则f′（x）=e^x-a≥0，

所以函数f（x）=e^x-ax-2在（-∞，+∞）上单调递增

若a＞0，则当x∈（-∞，lna）时，f′（x）=e^x-a＜0；

当x∈（lna，+∞）时，f′（x）=e^x-a＞0；

所以，f（x）在（-∞，lna）单调递减，在（lna，+∞）上单调递增。

（2）由于a=1，所以，（x-k）f′（x）+x+1=（x-k）（e^x-1）+x+1

故当x＞0时，（x-k）f′（x）+x+1＞0等价于k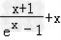＜（x＞0）①

令g（x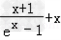）=，则g′（x）=

由（1）知，函数h（x）=e^x-x-2在（0，+∞）上单调递增，而h（1）＜0，h（2）＞0，

所以h（x）=e^x-x-2在（0，+∞）上存在唯一的零点，

故g′（x）在（0，+∞）上存在唯一的零点，

设此零点为α，则有α∈（1，2）当x∈（0，α）时，g′（x）＜0；

当x∈（α，+∞）时，g′（x）＞0；

所以g（x）在（0，+∞）上的最小值为g（α）

又由g′（α）=0，可得e^α=α+2

所以g（α）=α+1∈（2，3）

由于①式等价于k＜g（α），

故整数k的最大值为2。