如图所示，两根平行金属导轨MN、PQ相距为d=1.0m，导轨平面与水平面夹角为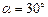
，导轨上端跨接一定值电阻R=1.6
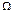，导轨电阻不计.整个装置处于方向垂直导轨平面向上、磁感应强度大小B=1.0T的匀强磁场中，金属棒ef垂直于MN、PQ静止放置，且与导轨保持良好接触，其长刚好为d、质量度m=0.10kg、电阻r=0.40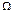，距导轨底端的距离
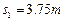。另一根与金属棒平行放置的绝缘棒gh长度也为d，质量为m/2，从轨道最低点以速度
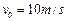沿轨道上滑并与金属棒发生正碰（碰撞时间极短），碰后金属棒沿导轨上滑
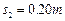后再次静止。测得从碰撞至金属棒静止过程中电阻R上产生的焦耳热为
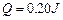。已知两棒与导轨间的动摩擦因数均为
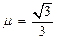，取
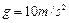，求：
（1）碰后瞬间两棒的速度
（2）碰后瞬间金属的加速度
（3）金属棒在导轨上运动的时间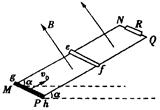
（1）
方向沿导轨向下
（2）
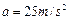方向沿导轨向下
（3）
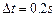
（1）碰前：
对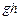
由动能定理：
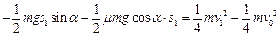① （1分）
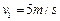………………………………………………………………② （1分）
碰后：
对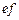
由能量守恒：
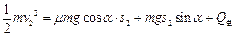………③ （2分）
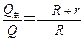…………………………………………………………④ （1分）
解方程组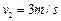
方向沿导轨向上…………………………………⑤ （1分）
相碰：由动量守恒 
……………………………⑥ （2分）
方向沿导轨向下…………………………………………⑦ （1分）
（2）
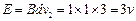………………………………………⑧ （1分）
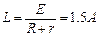………………………………………………………⑨ （1分）
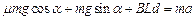……………………………………⑩ （1分）
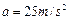方向沿导轨向下…………………………………………11（1分）
（3）
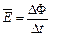………………………………………………………12（1分）
…………………………………………13 （1分）
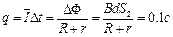…………………………………14（1分）
由动量定理：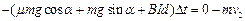
…………15（2分）
……………………………………………… 16（1分）
解方程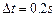…………………………………… 17（1分）