问题
计算题
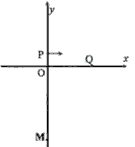
如图所示,在第一象限有一均强电场,场强大小为E,方向与y轴平行;在x轴下方有一均强磁场,磁场方向与纸面垂直。一质量为m、电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场,在x轴上的Q点处进入磁场,并从坐标原点O离开磁场。粒子在磁场中的运动轨迹与y轴交于M点。已知OP=l,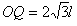 。不计重力。求
。不计重力。求
(1)M点与坐标原点O间的距离;
(2)粒子从P点运动到M点所用的时间。
答案
解:(1)带电粒子在电场中做类平抛运动,在y轴负方向上做初速度为零的匀加速运动,设加速度的大小为a;在x轴正方向上做匀速直线运动,设速度为v0,粒子从P点运动到Q点所用的时间为t1,进入磁场时速度方向与x轴正方向的夹角为θ,则
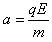 ①,
①,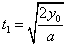 ②,
②,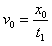 ③
③
其中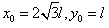 ,又有
,又有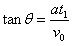 ④
④
联立②③④式,得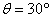
因为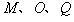 点在圆周上,
点在圆周上,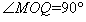 ,所以MQ为直径。从图中的几何关系可知
,所以MQ为直径。从图中的几何关系可知
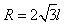 ⑥,
⑥,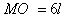 ⑦
⑦
(2)设粒子在磁场中运动的速度为v,从Q到M点运动的时间为t2,则有
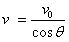 ⑧,
⑧,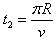 ⑨
⑨
带电粒子自P点出发到M点所用的时间为t为 ⑩
⑩
联立①②③⑤⑥⑧⑨⑩式,并代入数据得