问题
连线题
已知函数f（x）=ax2+1（a＞0），g（x）=x3+bx 。
（1）若曲线y=f（x）与曲线y=g（x）在它们的交点（1，c）处具有公共切线，求a、b的值；
（2）当a2=4b时，求函数f（x）+g（x）的单调区间，并求其在区间（-∞，-1）上的最大值。
答案
解：（1）f（x）=ax2+1（a＞0），
则f'（x）=2ax，k1=2a，
g（x）=x3+bx，则f'（x）=3x2+b，k2=3+b，
由（1，c）为公共切点，
可得：2a=3+b ①
又f（1）=a+1，g（1）=1+b，
∴a+1=1+b，即a=b，
代入①式可得：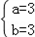
。
（2）由题设a2=4b，
设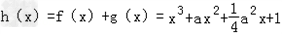
则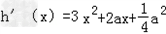
，
令h'（x）=0，解得：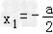
，
；
∵a＞0，
∴
，
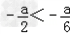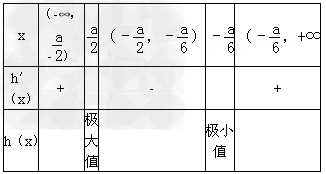
①若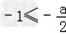
，即a≤2时，最大值为
；
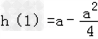②若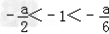
，即2＜a＜6时，最大值为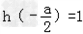
③若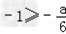
时，即a≥6时，最大值为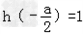
综上所述：当a∈（0，2]时，最大值为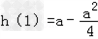
；
当a∈（2，+∞）时，最大值为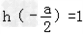
。