问题
计算题
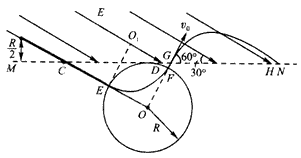
如图所示，在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场，电场区域足够宽，场强大小为E。在MN下方有一半径为R的圆形区域，圆心为O，圆O与MN相切于D点，圆形区域内分布有垂直纸面向里的匀强磁场。在MN上有一点C，圆心O与C点的连线和电场线平行，在OC的延长线上有一点P，P点到边界MN的垂直距离为0.5R。一质量为m、电荷量为q的带正电的粒子从P点静止释放。已知圆形磁场的磁感应强度大小为
，不计粒子的重力。求：
（1）粒子在磁场中的运动半径r；
（2）粒子最终离开电场时的速度v。
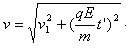
答案
解：（1）设粒子从C点射出电场时速度为v1
由动能定理
，所以v1=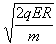
在磁场中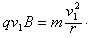
又由题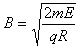
，联立得r=R
（2）粒子从E点进入磁场，从F点射出磁场，运动轨迹如图所示，轨迹的圆心为O1。由几何关系可知∠FO1E=90°。即粒子在磁场中速度偏转了90°，射出磁场时速度方向与MN夹角为60°，与电场线方向垂直粒于从G点垂直进入磁场，作类平抛运动，从H点射出电场，设从G运动到H所用时间为t'，则
在电场中有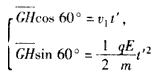
联立得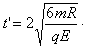
所以射出电场时的速度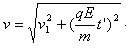
代入数据得