问题
解答题
已知函数f（x）=（x+1）lnx﹣x+1．
（1）若xf'（x）≤x2+ax+1，求a的取值范围；
（2）证明：（x﹣1）f（x）≥0
答案
解：（1）函数的定义域为（0，+∞）求导函数，
可得
，
xf?（x）=xlnx+1，
题设xf（x）≥x2+ax+1等价于lnx﹣x≤a，
令g（x）=lnx﹣x，则g（x）=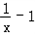
．
当0＜x＜1时，g
（x）＞0；
当x1时，g（x）＞0，x=1是g（x）的最大值点，
g（x）≤g（1）=﹣1．
综上，a的取值范围是[﹣1，+∞）
（2）由（1）知，g（x）*g（1）=﹣1，
即lnx﹣x+1≤0；
当0＜x＜1时，f（x）=（x+1）lnx﹣x+1
=xlnx+（lnx﹣x+1）
当x＞1时，f（x）=lnx+（xlnx﹣x+1）
=lnx+x（lnx+
﹣1）
所以（x﹣1）f（x）≥0