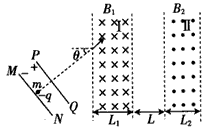
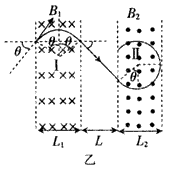
扭摆器是同步辐射装置中的插入件,能使粒子的运动轨迹发生扭摆。其简化模型如图:I、Ⅱ两处的条形 匀强磁场区边界竖直,相距为L,磁场方向相反且垂直于纸面。一质量为m、电量为-q、重力不计的粒子,从靠 * * 行板电容器MN板处由静止释放,极板间电压为U,粒子经电场加速后平行于纸面射入I区,射入时速度与水平方向夹角θ=30°。
(1)当I区宽度L1=L、磁感应强度大小B1=B0时,粒子从I区右边界射出时速度与水平方向夹角也为30°,求B0及粒子在I区运动的时间t。
(2)若Ⅱ区宽度L2=L1=L、磁感应强度大小B2=B1=B0,求粒子在I区的最高点与Ⅱ区的最低点之间的高度差h。
(3)若L2=L1=L、B1=B0,为使粒子能返回I区,求B2应满足的条件。
(4)若B1≠B2、L1≠L2,且已保证了粒子能从Ⅱ区右边界射入。为使粒子从Ⅱ区右边界射出的方向与从I区左 边界射出的方向总相同,求B1、B2、L1、L2之间应满足的关系式。
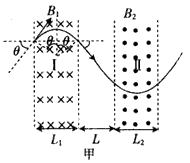
解:(1)如图甲所示,设粒子射入磁场I区的速度为v,在磁场I区中做圆周运动的半径为R1,由动能定理和牛顿第二定律得:
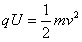 ,
,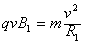
由几何知识得:L=2R1sinθ
联立解得: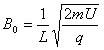
设粒子在磁场I区中做圆周运动的周期为T,运动的时间为t,则:
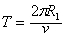 ,
,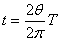
联立解得: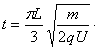
(2)设粒子在磁场Ⅱ区做圆周运动的半径为R2,由牛顿第二定律得: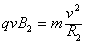
由几何知识可得:h=(R1+R2)(1-cosθ)+Ltanθ
联立解得: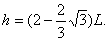
(3)如图乙所示,为使粒子能再次回到I区,应满足R2(1+sinθ)<L[或R2(1+sinθ)≤L]
解得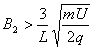 (或B2≥
(或B2≥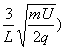
(4)如图丙(或图丁)所示,设粒子射出磁场I区时速度与水平方向的夹角为α,由几何知识可得:
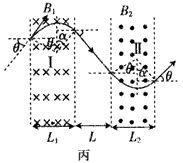

L1=R1(sinθ+sinα)[或L1=R1(sinθ-sinα)]
L2=R2(sinθ+sinα)[或L2=R2(sinθ-sinα)]
解得:B1R1=B2R2
联立解得:B1L1=B2L2
