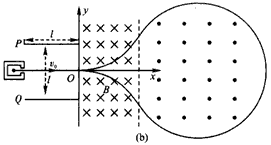
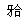如图(a)所示,建立xOy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一、四象限有一宽度一定的匀强磁场,磁感应强度为B,方向垂直于xOy平面向里。位于极板左侧的粒子源沿x轴向右连续发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~4t0时间内两板间加上如图(b)所示的电压(不考虑极板边缘的影响)。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、t、t0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)
(1)求两板间的电压U0;
(2)0~t0时间内射入两板间的带电粒子都能够从磁场右边界射出,求磁场的最大宽度;
(3)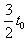 时刻射入两板间的带电粒子进入磁场和离开磁场时的位置坐标;
时刻射入两板间的带电粒子进入磁场和离开磁场时的位置坐标;
(4)若两板间电压为0,请设计一种方案:粒子源沿x轴向右连续发射的带电粒子,经过y轴右边的几个有边界的磁场后,带电粒子又返回粒子源。
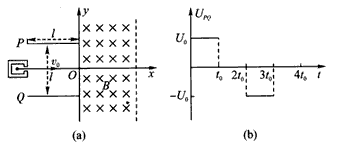
解:(1)t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场,则在两极板间,y轴方向
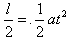 ,其中
,其中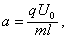 t=t0
t=t0
解得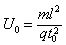
(2)经过分析,0-t0时间内,t0时刻射入两板间的带电粒子进入磁场并能够从磁场右边界射出,则其他粒子也能从磁场右边界射出,t0时刻射入两板间的带电粒子,在两板间匀速运动,并从O点沿+x方向射入磁场,在磁场中的运动半径为R,qv0B=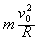 ,得又l=v0t0
,得又l=v0t0
则磁场的最大宽度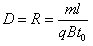
(3)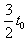 时刻射入两板间的带电粒子,在
时刻射入两板间的带电粒子,在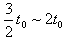 时间做匀速直线运动,在
时间做匀速直线运动,在 向上偏转
向上偏转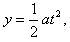 其中
其中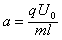 0
0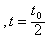 ,得y=
,得y=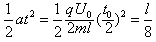
故进入磁场时的位置坐标为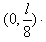
从y轴离开磁场与进入磁场的距离
又l=v0t0,△y= 
离开磁场的位置坐标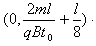
(4)由对称性可设计如图(b)所示的磁场区域,粒子源沿x轴向右连续发射的带电粒子,经过y轴右边的几个有边界的磁场后,带电粒子又返回粒子源