问题
计算题
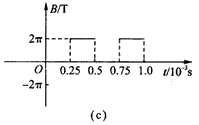
在如图(a)所示的平面直角坐标系xOy中，存在沿x方向按如图(b)所示规律周期性变化的匀强电场，沿x轴正向为正。沿垂直于xOy平面指向纸里的方向存在按如图(c)所示规律周期性变化的匀强磁场。在图(a)中坐标原点O处有带正电的粒子，从t=0时刻无初速度释放。已知粒子的质量m=5×10-10 kg，电荷量q=1×10-6 C，不计粒子的重力。求：
（1）t=0.25×10-3 s时粒子的速度及位置；
（2）t=1×10-3 s时粒子的位置坐标；
（3）t=8×10-3 s时粒子的速度。
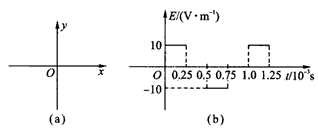
答案
解：（1）在笫一个t0=0.25×10-3 s内粒子的加速度a满足：qE=ma
末速度v1=at0=5 m/s
沿x轴正方向运动轴正向运动L1＝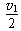
t0＝6.25×10-4 m
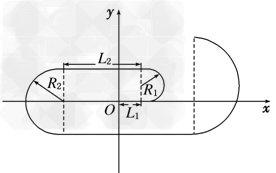
（2）在0.25×10-3-0.5×10-3 s内粒子做匀速圆周运动
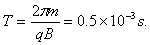
故粒子在0.25×10-3 s这段时间内运动了半个圆周
圆周运动的半径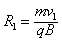
在0.5×10-3~0.75×10-3 s内粒子沿x轴负方向匀加速运动末速度大小v2=v1+at0=2v1
位移大小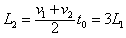
在0.75×10-3~1×10-3 s内粒子做匀速圆周运动，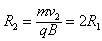
末位置坐标：x=-（L2-L1）=-1.25×10-3 m， y=-（2R2-2R1）= -8×10-4 m
（3）粒子在8×10-3 s内16次加速，每次速度增加v1，故在8×103 s 时粒子的速度v=16v1，v=80 m/s，方向沿x轴正方向